home \ courses \ music theory \ page 11

The circle of fifths

You may have noticed somdething interesting looking at the scales on the previous page. The scale of C major has no sharps, the scale of G major has one sharp: the F#. The scale of D has two sharps: F# and C#.
There is a pattern!
If you start at C, the distance to G is five (C1 D2 E3 F4 G5). There is one sharp in G major: (the F#)
If you start at G, the distance to D is five (G1 A2 B3 C4 D5). There are two sharps in D major (the F# and C#)
If you start at D, the distance to A is five (D1 E2 F3 G4 A5). There are three sharps in A major (the F# and C# and G#)
This pattern continues.

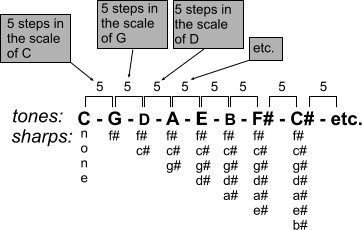
If you take following sequence of tones:

C - G - D - A - E- B - F# - C# - G# - D# - A#

You can add sharps:

C: no sharps
G: 1 sharp (f#)
D: 2 sharps (f# c#)
etc.

In every step a sharp is added. The order of the sharps is:

f# - c# - g# - d# - a# - e# - b# - f## - c## - g##

There are two new things here.

First, there are "double sharps". Sometimes they are indicated with a small cross. So f## = fx. These double sharps exist because we have the rule of every letter occuring only once.
If you thake the scale og G#, and apply the distances netween the tones as we did before, you'll see that the F should be two semitones higher in order to be correct. So you'll need two sharps. F## sounds the same as G!

The other thins is the e# and b#. Same reason: if you have the scale of f#, the e isn't high enough. So it needs a sharp. E# sounds the same as the F!

Let's put this in a scheme:

Before we saw that scales sometimes haves harps, sometimes they have flats. For the flats a similar system exists.
To get an overview of the flats, you have tot mirror the sequence of tones. If we start with the C, we put it at the right side. From C to G is 5. But what comes before C?<

The answer is "F". So we get:

F - C : from F to C is five steps.

Before the F we have Bb (B flat) : from Bb to F is five steps.

Bb - F - C

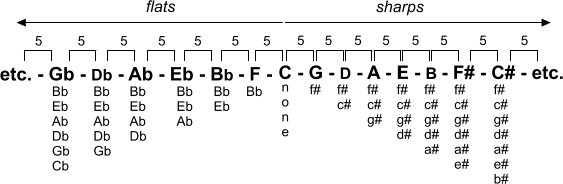
This is the sequence:

Gb - Dd - Ab - Eb - Bb - F - C

just as with sharps, every step (to the left this time) gets one extra flat. The order of the flats is:

Bb, Eb, Ab, Db, Gb, Cb

Let's put this in a scheme as well:

Now, let's combine the two:

To get a better overview, it is common to put this scheme in a circle, the circle of fifths. The principle of such a circle is exactly the same as the horizontal overview above.

So there are two ways to build scales: using the distances between the tones, or using the circle of fifths. To approaches, same result, use what ever suit you best!

<<< Previous page   |   Next page >>>