home \ courses \ music theory II \ page 7

Intervals and scales

We have looked at the scale of C major many times. The reason is clear: it is the easiest scale. Let's look at the scale of C again, and focus on the relations/distances of the tones:

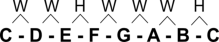
In part I we looked at the distance between the tones as wholes and semitones. We could also say that the distances are major and minor seconds. That however wouldn't serve any purpose.

What does make sense is to look at the intervals starting at the ground tone (tonica). If we do that, we have the following intervals:

• C-C perfect unison
• C-D major second
• C-E major third
• C-F perfect fourth
• C-G perfect fifth
• C-A major sixth
• C-B major seventh

Now look at that list and wonder why this is the scale of c major....

Let's jump to the minor scale of A. We choose A because it is the easiest minor scale (without flats and sharps). These are the intervals:

• A-A perfect unison
• A-B major second
• A-C minor third
• A-D perfect fourth
• A-E perfect fifth
• A-F minor sixth
• A-G minor seventh

Note that the third, sixth and seventh are minor.

Despite that the only really important difference between major and minor scales is the third. There are minro scales with a major sicth and/or seventh, but a minor scale with a major third will never exist.
There will be a separate part in this course about advanced scales, let it rest for now.

In summary, you can say thet a major scale has a perfgect unison, major second, major thoird, perfect fourth, perfect fifth, major sixth and major seventh:

A minor scale has a perfect unison, a major second, a minor third, a perfect fourth, a perfect fifth, a minor sixth and a minor seventh:

Major scales

We can apply this interval knowledge on other scales. Let's look at the scale of D major:

• perfect unison: D-D
• major second: D-E
• major third: D-F#
• perfect fourth: D-G
• perfect fifth: D-A
• major sixth: D-B
• major seventh: D-C#

So the scale of D-major is:
D-E-F#-G-A-B-C#

Minor scales

Let's do the same for a minor scale, the scale of G-minor:

• perfect unison: G-G
• major second: G-A
• minor third: G-Bb
• perfect fourth: G-C
• perfect fifth: G-D
• minor sixth: G-Eb
• minor seventh: G-F

The scale of G-minor is:
G-A-Bb-C-D-Eb-F

As you can see, it's all connected! And not onlys scales and intervals, also chords, which is the subject of the next part of this course.

Scales, intervals and chords are inextricably linked!

<<< Previous page   |   Home